On the back of an earlier post on Transforming Functions, I thought I might share some other A/A* lessons I have taught recently. Please note, what has worked well for me and my students, may not work well for you and your students. The idea of the post is to give people a starting point and if it inspires just one idea, then it has been worthwhile! I would also be interested in other people’s ideas/approaches, please use the comments section below to share these. Also, if you are just looking for resources on proof, try Jo Morgan’s (@mathsjem)fantastic resourceaholic website.
I taught algebraic proof to my year 11s a few weeks ago over a period of a couple of lessons. I started with a bit of number magic to ‘hook’ them and although my trick was met with groans and rolled eyes (they’re a lovely bunch – really!) they were still curious as to how I did it. I then talked to them about what a proof is and why I enjoy proof, particularly algebraic proof, so much. We discussed some famous proofs and in particular Fermat’s last theorem. I then asked them to use algebra to prove that my magic trick would always work which they were able to do with very little intervention from me.
We then explored what would happen when carrying out different calculations with odd/even numbers. I explained that we can try lots of different numbers to help us come up with a ‘conjecture’, but this doesn’t count as a mathematical proof. I demonstrated how some of these things could be proven using multi-link cubes (numicon would work well for this) and then we moved onto looking at how we can use algebra to represent different types of numbers. The next part of the lesson worked particularly well:
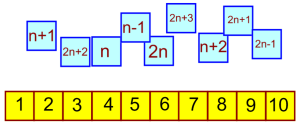
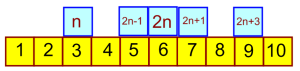
We used this number line on the interactive whiteboard to discuss what each of the expressions could represent as long as ‘n’ represented an integer. This proved to be a powerful visual for the remainder of the lesson (I was annoyed with myself later on for missing a trick – I will definitely create a 1-20 number line, with the expressions on tiles, to give the students to play with in time for the next time I teach this). See the example below for how we decided on how we could represent 3 consecutive odd numbers:
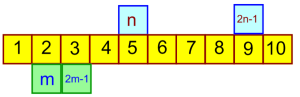
Below shows how representing ‘any two odd numbers’ would require a second variable:
We then went on to use these tools to prove various conjectures, before finally, when they were ready, looking at some challenging GCSE style proof questions. Each time, I encouraged them to try things out with numbers first so that they can get a feel for what they are trying to achieve. See below for full lesson which you can download from here (Smart notebook). I will also be using this proof revision mat for revision in a couple of weeks.
If you have any comments, thoughts or ideas, please share below.
Useful from twitter
@MathedUp @mathsjem You might want to see how your students respond to this proof Q (from BSRLM 24,1) pic.twitter.com/lgwovRkDBY
— Professor Smudge (@ProfSmudge) April 8, 2015
@MathedUp @mathsjem Thanks. It was used in the Longitudinal Proof Project. There’s a similar geometry task: http://t.co/RFBdEWwW2k — Professor Smudge (@ProfSmudge) April 8, 2015
@MathedUp A few more examples. Full document on http://t.co/3BaPBxJizd pic.twitter.com/XOCrgeRK4c
— Mark the Math (@MarkK58) April 8, 2015
@NMPartnershipUK @mathsjem @MathedUp Or this follow-up study: http://t.co/S8fnfAIS17
— Professor Smudge (@ProfSmudge) April 9, 2015